We have some pretty exciting news! 🤩 Since 2022-02-22, we’ve been using a new and improved ranking as the default sorting for our front page at Recommend.Games.
… What do you mean, you haven’t noticed there’s a R.G ranking? You know, that thing that’s referenced in the statistics? … You haven’t ever opened that view?!? 😱
OK, let’s back up for a second. R.G’s primary purpose is a recommendation engine, that is, finding personalised game recommendations based on a user’s preferences (in this case as expressed through their BoardGameGeek ratings). But we want to show some games to the users immediately when they load the start page, before entering their user name. Think of these games as recommendations for… anyone. What games would you recommend to a person if you didn’t know anything about their taste? This is the implicit purpose of any “Top X entities” list. Since this is a recommendation site, we’d like to make this claim explicit, so the R.G ranking has always been those “recommendations for everyone”. What’s changed is the way those recommendations are calculated.
Recommendations are based on a technique known as collaborative filtering. Basically, the algorithm tries to learn the users’ preferences based on their ratings, find users with similar tastes, and then recommend new games that user might like. R.G uses Apple’s implementation Turi Create for its recommendations, which does a lot of magic 🪄 under the hood. One of those magic tricks is that it offers recommendations for users it doesn’t know anything about. The algorithm treats those users as new and offers some default recommendations that should be a good starting point for anybody, without any particular context. It’s exactly those recommendations that R.G has been using for years as our ranking and default sorting.
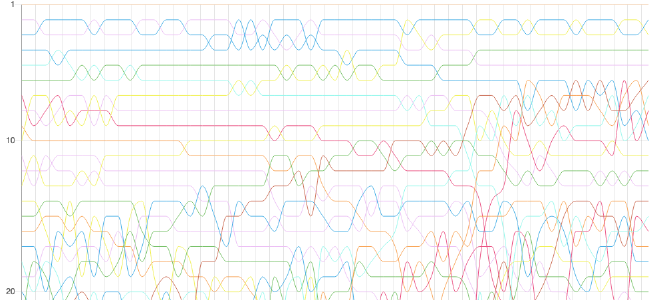
So, why change this and create a new ranking? There’s a number of problems with the old ranking. For one, it’s really swingy.1 Seriously, just take a look at the history:2
Maybe more importantly, the exact algorithm to determine those recommendations for new users is extremely obscure. There’s been a long-standing ticket to find out what’s going on. The answer isn’t documented anywhere, but you can find it somewhere in these lines of code. Let me know if you can make sense of them, I’ve simply given up at some point.
Instead, I wanted to create a new ranking which I can at least explain. So here goes:
The basic idea is to calculate the recommended games for all users, and then average those rankings. Those averages would become the Recommend.Games rankings.
That sounds simple and intuitive, but, as the saying goes, the devil is in the details. For starters, there are over 100,000 games in the BoardGameGeek database, and over 400,000 users with at least one rated game. Calculating all recommendations for all users would therefore mean over 40 billion user–game pairs. That’s a lot. 😅 But really, we don’t care if a game is the 1,000th, 10,000th or 100,000th highest rated game. Instead, we only recommend the top 100 games for each user. The highest game on that list receives 100 points, the next 99, and so on, until the 100th game receives a single point from that user. All other games will be awarded 0 points. The we can simply average those points across all users, and voilà, those scores become the R.G rankings. 🤩
… Except that’s still not the whole story. I wasn’t happy about the idea of a user who fifteen years ago left a single rating being equally important as someone who played and rated hundreds of board games over two decades of BGG history. That’s why I tried to model the “trust” we should put in different users’ ratings. The idea here would be that we should trust a user’s rating more if two things are true:
- They are a regular contributor to BGG, i.e., rate, log plays etc at least once a month over a long period of time.
- They should rate games with a reasonable distribution, i.e., on a nice bell curve.
For the first point we count each calendar month that the user was active on BGG (e.g., rated a game, logged a play, updated their collection). Then we take the logarithm (base 2) of that number – this means the score will rise quite rapidly in the first year of BGG activity, but then flatten out quite quickly. The goal is not to treat newcomers too harshly. Note that \(\log_2 1 = 0\), so new users with only one month of activity will start with zero trust and consequently not be considered in the rankings calculations.
The second point is a little trickier. Mathematically speaking, we want to assess how closely a user’s ratings follow a normal distribution. There are a couple of neat statistical tests that do that, the one that’s considered best is the Shapiro–Wilk test. What we care about is a number between 0 and 1 that somehow measures how much a user’s rating distribution resembles a bell. Take, for instance, Tom Vasel’s ratings. He clearly users a nice spread for his ratings:
If on the other hand a user only ever rates games with a 10, never any other score, their factor would be 0, and again, they wouldn’t take part in the R.G rankings calculations.
So, long story short, we have those two factors that are supposed to describe how much we can trust a user’s ratings. We can now multiply them with each other, and the higher the score, the higher will be our trust in their ratings, and consequently, the more weight their “vote” will have when calculating the R.G ranking.
But before we go there, what users do we trust the most? Many of the highest scores actually belong to pretty random users, so I’m not comfortable exposing them here, but it’s interesting to compare some of the “celebrities” in the hobby (and yours truly):
| User | Rank | Trust |
|---|---|---|
| W Eric Martin (BGG news) | 21 | 7.376 |
| Engelstein (Ludology) | 77 | 7.227 |
| Tomvasel (Dice Tower) | 312 | 7.009 |
| Aldie (BGG founder) | 1889 | 6.544 |
| Jameystegmaier (Stonemaier) | 3213 | 6.343 |
| Jonpurkis (Actualol) | 3628 | 6.296 |
| Bohnanzar (Uwe Rosenberg) | 8801 | 5.848 |
| Markus Shepherd 🤓 | 16207 | 5.453 |
| Quinns (SU&SD) | 16958 | 5.421 |
| Phelddagrif (Richard Garfield) | 67960 | 3.981 |
| Cephalofair (Isaac Childres) | 75010 | 3.833 |
| Elizharg (Elizabeth Hargrave) | 108248 | 3.156 |
My opinions on board games having more weight than Quintin Smith’s sure feels good. 🧐
-
In case you’re curious: The reason why the recommendations are so swingy is because they aren’t precisely calculated, but merely approximated by an algorithm called stochastic gradient descent, which is inherently non-deterministic. ↩︎
-
And this is even a smoothed version of the rankings: It uses the average score of one week to determine the ranking in that plot. ↩︎